【本書の内容】
線形代数(ベクトル・行列の基本から特異値分解)について、Pythonのプログラムをもとにわかりやすく解説した書籍です。線形代数の基礎理論をPythonによる具体例を交えて解説しているので、実際の挙動を見ながら基礎理論の知識を習得できます。
【本書の特徴】
・実際にプログラムで数値を入れて線形代数の計算結果を確認できる
・プログラムで結果を見ながら学習できるので幾何学的にイメージできる
【対象読者】
・Python を使いながら線形代数を学びたい学生、文系エンジニア
・線形代数の基礎を学びなおしたいエンジニア
【本書で扱う線形代数の主なトピック】
・ベクトルの基礎
・行列の基礎
・線形方程式系の解を求める計算方法
・行列式の基礎
・部分空間の基礎
・直交の定義・直交基底の作成方法
・最小二乗法による線形回帰
・固有値・固有ベクトルの定義と具体的な計算方法
・行列を対角化する方法
・特異値分解の定理
【目次】
第0章 開発環境の準備
第1章 ベクトル入門
第2章 行列
第3章 線形方程式系
第4章 行列式
第5章 部分空間
第6章 直交性
第7章 固有値と固有ベクトル
第8章 特異値分解
【著者プロフィール】
かくあき
学生時代から数値解析を中心にPython,Matlab,Fortran,C,LISPなどのプログラミング言語を利用している。Pythonの普及の一助となるべく、Udemyで講座を公開。Kindle Direct Publishingで電子書籍を出版するなど、情報発信を行う。著書に『現場で使える!Python科学技術計算入門』『Pythonで動かして学ぶ! あたらしいベイズ統計の教科書』(いづれも翔泳社)がある。


基本となるベクトルや行列の概念から始まり、線形代数の応用として代表的な特異値分解まで、学習できます(なお複素数や微分の知識が必要な部分は扱っていません)。

Pythonの学習で利用されることが多いJupyter Notebookで、サンプルを動かしながら線形代数の基礎を学ぶことができます。
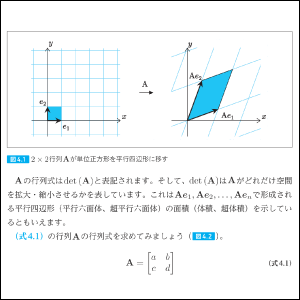
線形代数の基礎を理解しやすいよう、図や数式を利用して、わかりやすく解説しています。
第0章 開発環境の準備
0.1 Pythonのインストール
0.1.1 Anaconda Individual Editionのインストール
0.1.2 仮想環境を作成する
0.2 Jupyter Notebook
0.2.1 Jupyter Notebookとは
0.2.2 Jupyter Notebookを起動する
0.2.3 セルの操作
第1章 ベクトル入門
1.1 ベクトル
1.1.1 ベクトルの概念と幾何学的な解釈
1.1.2 Pythonでのベクトルの表現
1.2 ベクトルの基本的な演算
1.2.1 ベクトルの加算
1.2.2 スカラー倍
1.2.3 線形結合
1.2.4 ベクトル空間の要約
1.3 ベクトルの長さと内積
1.3.1 内積
1.3.2 内積の性質
1.3.3 ベクトルの長さ
1.3.4 ベクトル間の角度
第2章 行列
2.1 行列
2.1.1 行列の定義
2.1.2 Pythonでの行列の表現
2.2 基本的な行列の性質
2.2.1 行列の基本演算
2.2.2 ブロック行列
2.2.3 逆行列
2.2.4 転置
2.3 特徴的な行列
2.3.1 疎行列
2.3.2 対角行列
2.3.3 三角行列
第3章 線形方程式系
3.1 線形方程式系
3.1.1 線形方程式系の導入
3.1.2 行列形式の表現
3.2 線形変換
3.2.1 関数と変換
3.2.2 行列としての変換
3.2.3 線形変換の例
3.3 線形方程式系の解法
3.3.1 逆行列と解の関係
3.3.2 ガウスの消去法
3.3.3 ガウス・ジョルダンの消去法
3.3.4 解の個数の判定
3.3.5 逆行列の求め方
3.4 LU分解による線形方程式系の解法
3.4.1 LU分解
3.4.2 PLU分解
第4章 行列式
4.1 行列式
4.1.1 行列式の幾何学的な意味
4.1.2 行列式の定義
4.2 行列式の性質
4.2.1 基本的な性質
4.2.2 行基本変形と行列式
4.2.3 余因子行列
第5章 部分空間
5.1 部分空間
5.1.1 部分空間
5.1.2 線形従属、線形独立
5.2 行列の基本部分空間
5.2.1 零空間、左零空間
5.2.2 行空間、列空間
5.3 基底
5.3.1 部分空間の基底
5.3.2 列空間の基底の求め方
5.3.3 行空間の基底の求め方
5.3.4 零空間の基底の求め方
5.3.5 階数・退化次数の定理
第6章 直交性
6.1 直交行列
6.1.1 直交
6.1.2 直交行列
6.2 QR分解
6.2.1 グラム・シュミットの正規直交化法
6.2.2 QR分解
6.3 最小二乗法による線形回帰
6.3.1 単回帰
6.3.2 重回帰
第7章 固有値と固有ベクトル
7.1 固有値と固有ベクトル
7.1.1 固有値問題
7.1.2 固有値と固有ベクトルの求め方
7.1.3 重複度
7.2 対角化
7.2.1 基底変換
7.2.2 対角化
7.2.3 相似
7.2.4 行列の跡
7.2.5 行列のべき乗
7.2.6 直交対角化
第8章 特異値分解
8.1 特異値分解
8.1.1 特異値
8.1.2 特異値分解
8.1.3 特異値分解と基本部分行列
8.1.4 特異値分解の幾何学的解釈
8.2 特異値分解の応用
8.2.1 行列ノルム
8.2.2 特異値分解を用いたデータ圧縮
8.2.3 逆行列の計算
8.2.4 擬似逆行列